The Pauli Exclusion Principle
On the Connection between the Completion of Electron Groups in an Atom with the Complex Structure of Spectra (1925)
Although it may be hard to wrap your head around the strange behavior of quantum systems, the classical world we so complacently inhabit would shatter without it.
In 1925, Wolfgang Pauli published a paper that gave credence to the concept of electron spin. We have already gone over how the notion of quantum spin emerges naturally from how particles interact with magnetic fields. Pauli figured out how this property becomes fundamental in atomic structure.
His paper, titled "On the Connection between the Completion of Electron Groups in an Atom with the Complex Structure of Spectra," introduced a new quantum number that explained the peculiarities of atomic spectra and the periodic table. This breakthrough eventually led to the Pauli exclusion principle, a cornerstone of modern quantum physics.
The Mystery of Atomic Spectra
At the heart of Pauli’s investigation was the perplexing structure of atomic spectra. When atoms emit or absorb light, they do so in discrete spectral lines, corresponding to the quantized energy transitions of electrons.
However, many spectral lines exhibited fine structure—splitting into multiple closely spaced components. This is often known as Zeeman effect and was particularly evident in alkali metal atoms, where spectral lines formed doublets, a phenomenon difficult to explain using existing quantum theories.
Scientists like Alfred Landé and Robert Millikan suggested that the fine structure could be described by relativistic corrections to electron motion. Sommerfeld’s model, an extension of Bohr’s atom, introduced elliptical orbits and relativistic effects to explain these details, but something was still missing. Why did some spectral lines split into doublets, and why did certain elements exhibit anomalous Zeeman effects when placed in a magnetic field?
A New Quantum Number
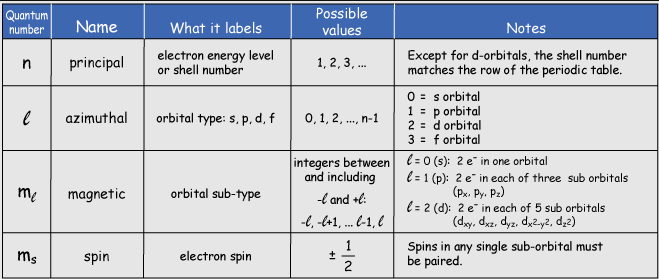
Pauli’s realization was that existing quantum numbers were insufficient to fully describe electron behavior in atoms. Up to that point, electrons were classified by three quantum numbers:
Principal quantum number (n) describes the electron’s energy level.
Azimuthal quantum number (l) relates to the shape of the orbital.
Magnetic quantum number (m) determines the orientation of the orbital in a magnetic field.
Pauli proposed an additional fourth quantum number, which would later be understood as electron spin (s). He suggested that electrons in an energy level exhibit an intrinsic ‘two-valuedness,’ meaning they could exist in one of two distinct states within the same orbital.
Mathematically, this new quantum number could take the values +1/2 or −1/2, effectively doubling the number of available electron states. This idea was revolutionary because it suggested that electrons possessed an intrinsic angular momentum that was fundamentally different from their orbital motion around the nucleus.
Pauli also demonstrated that the anomalous Zeeman effect could be understood if electrons had an intrinsic magnetic moment associated with their spin. Later, this idea was refined by Dirac’s relativistic quantum theory, which confirmed that electrons naturally possess spin with a g-factor (a dimensionless quantity that characterizes the magnetic moment and angular momentum of a particle) of approximately 2, precisely explaining the observed splitting of spectral lines.
The Exclusion Principle and Atomic Structure
Pauli’s most impactful conclusion was that no two electrons in an atom can share the same set of four quantum numbers. This is what we now call the Pauli Exclusion Principle.
It means that in a given atom, each electron must occupy a unique quantum state. This principle elegantly explained the periodic table’s structure. The completion of electron shells, which determines the chemical properties of elements, could now be understood in terms of the four quantum numbers.
Two electrons can share an orbital (same n, l, m) but must have opposite spins (+1/2 and −1/2). In addition, each energy level can hold a fixed number of electrons (e.g., the first shell can hold 2, the second can hold 8, etc.), leading to the periodicity observed in the elements.
This insight made intelligible quantum chemistry and solid-state physics, explaining why elements form specific bonds and why matter exhibits stability.
The Stability of Matter
At the time, Pauli’s proposal was a bold hypothesis, lacking a clear physical interpretation. It wasn’t until 1927 that Samuel Goudsmit and George Uhlenbeck formally introduced the idea of electron spin as a fundamental property of electrons. In 1928, Dirac’s equation fully integrated spin into quantum mechanics, showing that it arises naturally from the relativistic treatment of electrons.
The Pauli Exclusion principle applies only to fermions, not bosons like photons. This is due to the fact that fermions are described by antisymmetric wave functions.
In quantum mechanics, identical particles are indistinguishable. As a result, the probability distribution describing their behavior must remain unchanged if two particles are exchanged. However, the wave function itself may either remain the same or change sign.
Bosons have symmetric wave functions:
Fermions have antisymmetric wave functions:
Suppose we attempt to place two identical fermions in the same quantum state. Let their individual wave functions be ψ_1(x) and ψ_2(x). The total antisymmetrized wave function is given by the Slater determinant:
Now imagine both particles are in the same state, so ψ_1=ψ_2=ψ:
Since the two terms are identical,
The wave function vanishes identically if two fermions attempt to occupy the same quantum state. This is the rigorous mathematical formulation of the Pauli exclusion principle. The wave function results in a probability density of zero meaning such a configuration is physically impossible.
The exclusion principle seems to play a critical role in ensuring that reality exists. It ensures that electrons do not all collapse into the lowest energy state by limiting the number of electrons per orbital. As we have discussed with respect to degenerate matter obeying Fermi-Dirac statistics, the exclusion principle creates a powerful quantum pressure that counteracts gravitational collapse in dense astrophysical objects like white dwarfs and neutron stars.
Related Papers:
Bohr, N. (1923). Über die Anwendung der Quantentheorie auf den Atombau. I. Die Grundpostulate der Quantentheorie. Zeitschrift für Physik, 13, 117–165.
Bohr introduced the Aufbauprinzip (principle of gradual construction) in atomic structure, suggesting that electrons fill energy levels in a systematic way, leading to the periodic table’s organization. Pauli's work extended this principle by proposing that the completion of electron groups required a fourth quantum number (spin), ensuring no two electrons shared the same quantum state.Landé, A. (1924). Über den anomalen Zeemaneffekt und die Aufspaltung der Termniveaus. Zeitschrift für Physik, 25, 279–286.
Landé analyzed the anomalous Zeeman effect, where spectral lines split in a way not predicted by simple quantum number models. He introduced the Landé g-factor, suggesting an additional quantum property influencing magnetic behavior. Pauli built upon this, proposing that an electron’s two-valuedness (later understood as spin) was responsible for such anomalous spectral features.Stoner, E. C. (1924). The Distribution of Electrons among Atomic Levels. Philosophical Magazine, 48, 719–736.
Stoner revised Bohr’s electronic configurations, proposing that electron shells should be subdivided into groups with specific numbers of electrons, guided by empirical spectroscopic data. Pauli refined this idea by asserting that electron configurations obey an exclusion principle, limiting occupancy based on a fourth quantum number (spin).